Prims Algorithmus

In diesem Tutorial erfahren Sie, wie der Prim-Algorithmus funktioniert. Außerdem finden Sie Arbeitsbeispiele für den Prim-Algorithmus in C, C ++, Java und Python.

Der Prim-Algorithmus ist ein Minimum-Spanning-Tree-Algorithmus, der ein Diagramm als Eingabe verwendet und die Teilmenge der Kanten dieses Diagramms ermittelt

Bilden Sie einen Baum, der jeden Scheitelpunkt enthält
hat die minimale Summe von Gewichten unter allen Bäumen, die aus dem Diagramm gebildet werden können

Wie der Algorithmus von Prim funktioniert

Es fällt unter eine Klasse von Algorithmen, die als gierige Algorithmen bezeichnet werden und das lokale Optimum in der Hoffnung finden, ein globales Optimum zu finden.

Wir beginnen an einem Scheitelpunkt und fügen Kanten mit dem geringsten Gewicht hinzu, bis wir unser Ziel erreichen.

Die Schritte zum Implementieren des Prim-Algorithmus sind wie folgt:

Initialisieren Sie den minimalen Spannbaum mit einem zufällig ausgewählten Scheitelpunkt.
Suchen Sie alle Kanten, die den Baum mit neuen Scheitelpunkten verbinden, suchen Sie das Minimum und fügen Sie es dem Baum hinzu
Wiederholen Sie Schritt 2 so lange, bis wir einen minimalen Spannbaum erhalten

Beispiel für den Prim-Algorithmus

Beginnen Sie mit einem gewichteten Graphen

Wählen Sie eine Ecke mit

der kürzesten Kante Wählen Sie aus diesem Scheitelpunkt und fügen Sie

den nächsten Scheitelpunkt Wählen Sie noch nicht in der Lösung

Wählen Sie die nächste Kante noch nicht in der Lösung, wenn es mehrere Möglichkeiten gibt, wählen Sie eine zufällig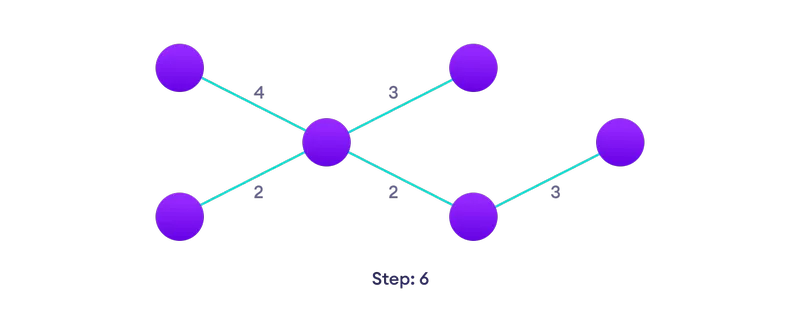

wiederholen , bis Sie habe einen Spannbaum

Prim's Algorithmus Pseudocode

Der Pseudocode für den Algorithmus von prim zeigt, wie wir zwei Sätze von Eckpunkten U und VU erstellen. U enthält die Liste der besuchten Scheitelpunkte und VU die Liste der nicht besuchten Scheitelpunkte. Nacheinander verschieben wir die Scheitelpunkte von Satz VU zu Satz U, indem wir die Kante mit dem geringsten Gewicht verbinden.

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

Beispiele für Python, Java und C / C ++

Obwohl die Adjazenzmatrixdarstellung von Graphen verwendet wird, kann dieser Algorithmus auch unter Verwendung der Adjazenzliste implementiert werden, um seine Effizienz zu verbessern.

Python Java C C ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

Prim's vs Kruskal's Algorithmus

Der Kruskal-Algorithmus ist ein weiterer beliebter Minimum-Spanning-Tree-Algorithmus, der eine andere Logik verwendet, um die MST eines Graphen zu ermitteln. Anstatt von einem Scheitelpunkt auszugehen, sortiert der Kruskal-Algorithmus alle Kanten von geringem Gewicht zu hohem und fügt weiterhin die niedrigsten Kanten hinzu, wobei die Kanten ignoriert werden, die einen Zyklus erzeugen.